Heat inactivation models fitting
Modelling thermal destruction of microbial populations can be split into several levels.
The first level is called the primary destruction model. It involves describing the destruction kinetics (changes to the size of the population over time). The model’s main parameter is the duration of the decimal reduction (D), which leads to a ten-fold reduction of the population size.
The secondary model describes the changes to the primary model parameter (D) caused by environmental factors. It takes account of the effect of the main factors such as temperature and pH.
Primary model to predict heat inactivation
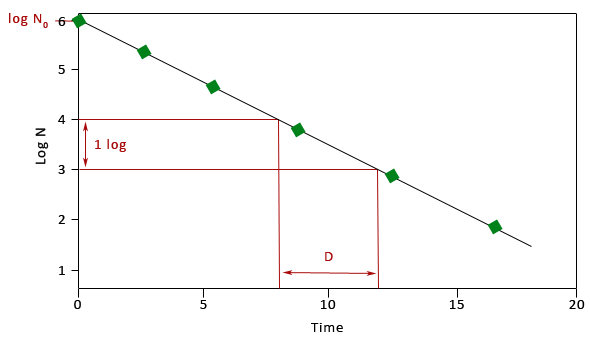
A primary model describes the evolution of the population size vs the heating time.
Heat destruction kenetic is often log-linear. Heat resistance is characterised by the ‘D-value’, i.e. the time that leads to a 10-fold reduction of surviving population.
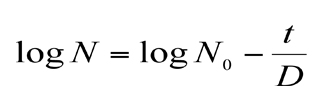
N0 : initial number of cells
t : heat treatment time
D : Decimal reduction time (heat resistance)
When heat destruction kinetics are not log-linear, a shape parameter (p) completes the model. So, D-value becomes ∂-value which is the first decimal reduction time :
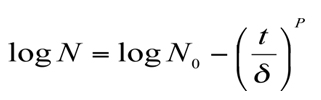
Secondary destruction models
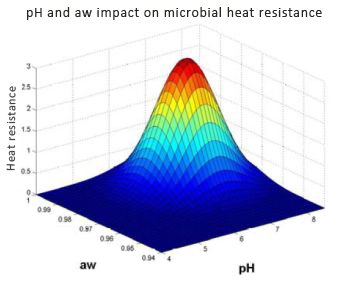
Physico-chemical factors impact
To describe physico-chemical factors impact on thermal destruction, modular approach consists to model each factor independently.
Each factor (pH and aw) affects heat resistance at 2 levels : The first one increases destruction during the heat treatment, and the second one inhibits the most damaged bacteria after heat treatment (respectively written X and X’ in the model below).
When the studied factors are temperature, pH and water activity, model can be written :
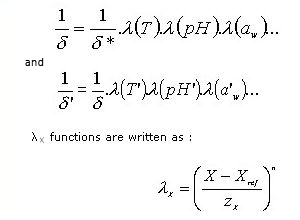
∂* is the first decimal reduction time in standard conditions (T, pH et aw), λX is the function related to the x factor.
∂ is the first decimal reduction time in studied environmental conditions.
Where :
X is the studied physico-chemical factor (written X during heat treatment, and X’ after heat treatment)
Xref is a reference value (for which ∂* has been estimated)
zX express the difference between X and Xref that leads to a 10-fold reduction of ∂*.



